Understanding the models made easier

Almost everything you never wanted to know about SEIR modelling of epidemics but probably should after 20 months of being made follow their predictions

When I have asked people about their favorite and least favorite subjects in school, there seems to be a pretty consistent top of the hate list:

1. Calculus

There are probably lots of reasons for this, but I think the main reason Calculus is on top is that it requires you to make a bit of a mental jump to understand it. If you don’t force your brain to wrap itself around its strange ideas then it will just seem like a large collection of random rules involving letters…

A long way down in levels of hate, but none the less in the number two slot we have:

2. Chemistry

I could be wrong, but I think Chemistry gets on the hate list because of lots and lots of failed experiments involving beakers, Bunsen burners leading to very smelly end results that were quite clearly wrong.

¹

Is there a point to this Stephen?

OK, yes, sorry.

Here we in November 2021, more than 20 months into a global pandemic and all the reactions to that pandemic are being driven by people with computer models.

The models they are using are called SEIR models, and, at their core, they are really just Calculus! Yes! The most dreaded of school subjects. You can be totally forgiven for not wanting to dig into the SEIR models and what they mean and how they work when you find out that they are basically Calculus… (readers of a sensitive disposition may want to skip to the next paragraph now) in fact they are what is known as a system of ordinary differential equations.

These models are controlling our world. I don’t think it is good enough that we just say “oh it’s calculus, we have no hope of understanding any of that”.

I can give you an outline of an understanding without using any calculus…

There’s a catch isn’t there?

It’s a fair cop, my explanation uses analogies from Chemistry… but I promise no Calculus!

Now before I continue, I should warn you that any numbers we might work out using a Chemistry understanding are unlikely to be correct, but what we will get is a feel for how changing various things will affect an epidemic wave. If you want more exact answers than “if we do this then that will move in this direction” then you’ll need to use the dreaded calculus, but you should have enough of an understanding to know the difference between someone saying something they don’t understand and somebody who understands the models.

So if you’re still here…

What is an SEIR model anyway?

If you want to model an epidemic, chances are you will use some form of SEIR model. The model is named for the different states the people being modelled can be in:

• S is for susceptible, these are the people who could catch the disease.

• E is for exposed, these are the people who have been exposed to the disease but are not yet spreading it.

• I is for infectious, these are the people who have caught the disease and are able to spread it to others.

• R is for recovered, these are the people who have recovered

  ²
  from the disease and are no longer spreading or susceptible to it.

There’s actually a whole family of these models with different names, for example the SEIRS model (note the extra S) is for diseases where the recovered become susceptible again after a period of time and the simpler SIR model is for diseases where you become infectious as soon as you are infected.

The chemistry understanding

I’m going to start backwards, because it’s easer that way.

The infectious do not stay infectious forever. They recover. If we were to write a chemical equation for what happens to the infectious we would have:

I → R

A chemistry graduate would instantly recognize this as what’s called a “first order reaction”.

³

This means that the rate of this reaction is proportional to the number of infectious people.

You could think of it this way, if we have two isolated islands with the same population and the only difference is that the first island has 100 infectious people and the second island has 50 infectious people then we expect the first island to have twice as many recovered per day as the second island.

The important thing that chemists remember about first order reactions is that they are described by what is known as a half-life. This is the amount of time it takes for the level of infected to reduce to half its current level (ignoring anything that might make more infectious)

So following the chain of reactions backwards we see that the exposed turn infected after a period of time:

E → I

This is also a first order reaction, so it too will have it’s own half-life.

A slightly wrong approximation that chemists will make when they have a chain of first order reactions is that the relative levels of each will be proportional to the half-life of each step.

You can think of it this way, if you are exposed on average for 5 days and then infectious on average for 10 days, then you will spend twice as long infectious as exposed. If everyone does that, then at any point in time there will be twice as many infectious as exposed. On the other hand if the half-life for the exposed state was 2 days then we’d expect five times as many infectious as exposed because 2:10 is the same as 1:5

Now if we used calculus we would predict that this will not be exactly true, but our intuition from this chemistry approximation will tell us the directions that things will move. If we can halve the infectious period then the level of infectious relative to exposed will also be halved.

Finally we need to look at how people become exposed. You get an exposed person when a susceptible person meets an infectious person, the infectious person remains infectious after the contact:

S + I → E + I

This is a different shape of reaction. It is what is known as a “second order reaction” because it involves the combination of two things, so the rate will depend on the levels of both people on the left hand side.

What a chemist will tell you about second order reactions is that unless you are extremely lucky with the levels, the rate will almost always be controlled (or limited) by the smaller of the two levels.

You can think of it like this, it doesn’t really matter if you have 1 million susceptible and 9 million recovered or 10 million susceptible and no recovered when there is only one infectious person there is a limit as to how many susceptible people they can meet on one day. We say that the rate is limited by the level of infectious people when that happens.

Similarly, when the level of susceptible is comparatively lower than the level of infectious, the rate will be limited by the level of susceptible people.

Now we can put all this together…

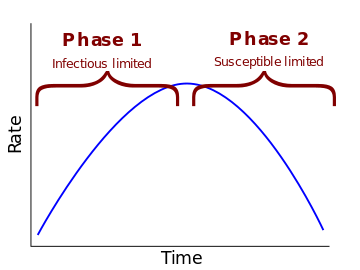
• Initially there are very few infectious, so the S + I → E + I step must be limited by the level of infectious. The more infectious there are the faster susceptible people will become exposed

• The infectious level will rise as long as the rate of the S + I → E + I step is faster than the rate of the I → R step.

• At some point the infectious level will rise enough that the S + I → E + I step becomes limited by the falling level of susceptible, from this point on-wards the level of infectious doesn’t really make that much of a difference we are limited by how many susceptible people there are remaining

If we were to sketch the level of infectious people we’d probably draw something like this:

When chemists say a reaction is first or second order they mean that is is proportional to the concentration (or level) of one or two of the components. The number that represents just how much in proportion is called the rate constant. Depending on the ratio of the rate constant for the S + I → E + I step with the rate constant of of the I → R step there will be a certain levels of susceptible below which the infectious level will never rise as the rate of the S + I → E + I step will always be lower than the rate of the I → R step when you start with that level of susceptible. Sure you will get a few of the susceptible infected, but the infection will never become an epidemic. We could call this level of susceptible as the “epidemic threshold” or “herd immunity”

⁴

Now you might ask what do those fancy Calculus models predict?

Here is a SEIR simulation for a disease with R0 of 2 where the half-life of exposed is 0.5 days and the half-life of infectious is 1 day. Purple is susceptible, red is exposed, green is infectious and light blue is recovered. The Y-axis is the fraction of the population, so 1 means 100%, 0.5 means 50% and so on.

• The exposed are about half as high as the infectious (I could bore you with the details) but before the peak exposed are around 0.78 of infectious and after the peak they are around 0.26 of infectious… the chemist will say: “on average that’s 0.52, see I was right”… to which all the mathematicians will go

  

• The susceptible never drops below 20%… that looks very much like the epidemic threshold that we had predicted

If people are interested, I can do another post that goes deeper and explore what a chemistry intuition says about the various interventions and when to apply them

⁵

… but I fear I lost most of you before we even got half way!

1. And let’s not forget the bits where it tries to sneak in some calculus under the name of Quantum Mechanics

2. In the darker corners of epidemiology R is also for removed, a euphamism for dead… I did say these were darker corners!

3. If it was a second order reaction we’d probably write it as I + I → 2R which would indicate that you only get recovered when an infectious person meets another infectious person… thankfully nobody has encountered a disease like that!

4. We could even do some approximate calculations to determine where the epidemic threshold would be… but I’d have to write down some differential equations - don’t worry we’d not do any calculus with them - to get an approximation… but i’ll not bore you with the details.

5. Hint: after the peak of infectious, there’s little point doing much of anything in the way of an intervention, you’re past the worst already